The Bedroom Desk
Edmonton Traffic Forecasting With a GNN (December 2025)

(Congestion + Volume, 15-60 Minutes Ahead)

Traffic forecasting title image Forecast UI showing controls, map, and top sites table

PREFACE

Over the last little while I learned two things:

  1. Edmonton has more traffic sensors than I expected.
  2. Graph neural networks will humble you repeatedly, and they do it with the calm indifference of an error message.

This project started as “I want to forecast congestion.” It turned into SSL certificates, missing files, broken deployments, baselines that refused to be beaten, and a map full of dots that only looked meaningful after I stared long enough.

ABSTRACT

Traffic is a graph problem that is often treated like a collection of independent time series. In reality, flow and congestion propagate through space: upstream changes appear downstream, and nearby corridors share load during transitions.

In this work, I build a spatio-temporal graph neural network (GNN) pipeline to forecast Edmonton traffic volume and a congestion proxy 15-60 minutes ahead using City of Edmonton sensor data aggregated into 15-minute intervals. Sensors are modeled as nodes; edges are defined by geographic proximity using k-nearest neighbors; temporal evolution is modeled with a recurrent unit over historical windows.

The main result is blunt: the system produces forecasts, but it does not meaningfully outperform a persistence baseline at short horizons. Residual forecasting (predicting deviations from the last observed value) yields small improvements at longer horizons and during rush hour, but the overall gains are marginal. The project mostly demonstrates how hard it is to extract signal beyond “the next hour resembles the last 15 minutes,” especially with limited data and an approximate graph.

INTRODUCTION

Forecasting traffic sounds simple: predict what happens in the next hour. In practice, traffic exhibits strong periodicity (commute cycles), abrupt exogenous shocks (incidents, weather), and spatial coupling (bottlenecks spill, routes substitute).

Many baseline approaches treat each sensor independently. That is workable, but it ignores the spatial structure implied by the road system. A slowdown is rarely isolated.

GNNs provide a way to learn from relational structure while modeling temporal dynamics. The goal here was straightforward:

It mostly worked, in the sense that the pipeline runs. It mostly failed, in the sense that the city does not care.

BACKGROUND

Graphs encode entities (nodes) and relationships (edges). In this project:

A simple GCN update can be written as:

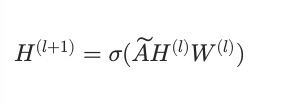
GCN update equation

where A_tilde is a normalized adjacency matrix, H is the node representation matrix, W are learnable weights, and sigma is a nonlinearity.

Traffic forecasting also requires time modeling. Spatial edges define possible influence; temporal structure defines when influence matters.

DATA

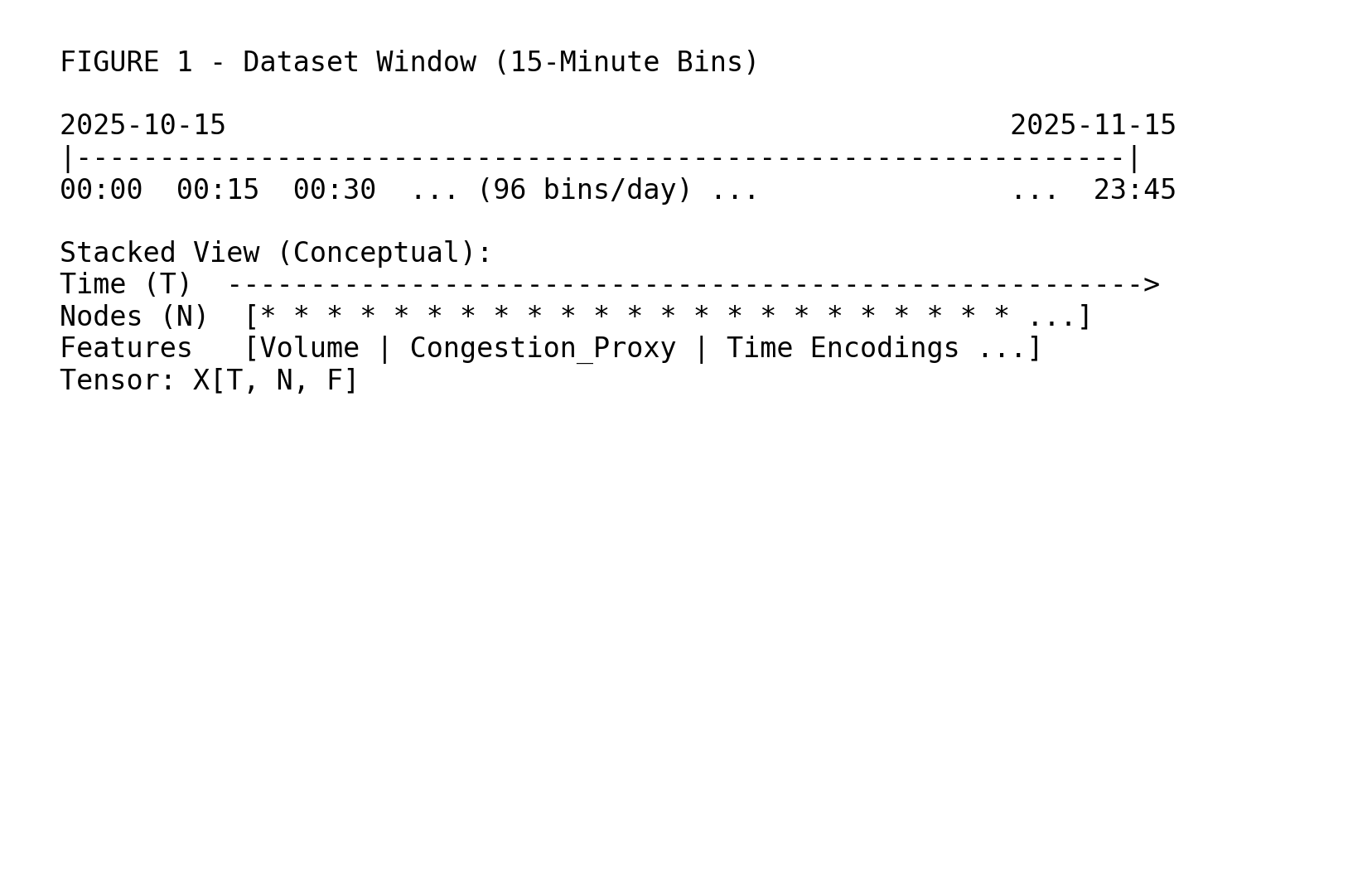
I used City of Edmonton open data traffic sensor records aggregated into 15-minute bins. Each row corresponds to a sensor site and time interval.

I constructed a tensor:

X in R^(T x N x F)

where:

I trained on a window like 2025-10-15 -> 2025-11-15. A month of data is enough to learn daily cycles. It is not enough to learn the city’s rare moods.

Figure 1 - Dataset Window (15-Minute Bins)

GRAPH CONSTRUCTION

I did not reconstruct the road network. Instead, I used a pragmatic geographic graph:

This graph is a convenience approximation: it encodes local correlation, not actual connectivity.

Conceptually, the graph looks like a local neighborhood mesh: each site is tethered to a small ring of nearby sites, forming overlapping clusters.

Nodes: {v1, v2, …, vN} Edges: (vi, vj) if vj is in kNN(vi)

Figure 2 - kNN Graph (Conceptual Geometry, Not an Edmonton Map) Graph construction visualization

MODEL

Baseline: Persistence

The persistence model predicts the last observed value:

x_hat(t+h) = x(t)

It is simple and extremely strong for short horizons.

Attempt 1: Direct Forecasting

The first model predicted absolute future values directly using a spatio-temporal architecture (GCN + temporal component). Training behavior looked reasonable: loss decreased and gradients behaved.

Performance did not. MAE was worse than persistence, especially at 15 minutes. The model learned to be confident about being slightly wrong.

Residual Forecasting

To avoid wasting capacity on learning continuity, I switched to residual prediction:

x_hat(t+h) = x(t) + delta(t+h)

where the network outputs delta(t+h).

This reframes the task: persistence is treated as the default, and the model learns corrections during transitions (ramp-up, ramp-down) and spatial spillover.

ARCHITECTURE

Spatio-Temporal Residual Model (GCN + GRU)

Given a history window of length L:

  1. Apply graph convolution at each time step (spatial mixing)
  2. Feed per-node embeddings through a GRU across time (temporal state)
  3. Output delta for multiple horizons (15/30/45/60 minutes)
Figure 3 - Pipeline (Spatio-Temporal Residual Forecasting)

EXPERIMENTS

Setup

Results

The baseline remained dominant at short horizons. Residual forecasting produced marginal improvements at longer horizons.

Multi-Horizon Volume MAE (vehicles per 15 min):

Rush-Hour Only:

Interpretation: small gains at 45-60 minutes, slightly larger in rush hour, essentially a tie at 15 minutes.

If this reads like a non-result, it is. The baseline is the closest thing traffic has to a philosophy.

Figure 4 - MAE vs. Horizon (Lower Is Better) [Schematic]

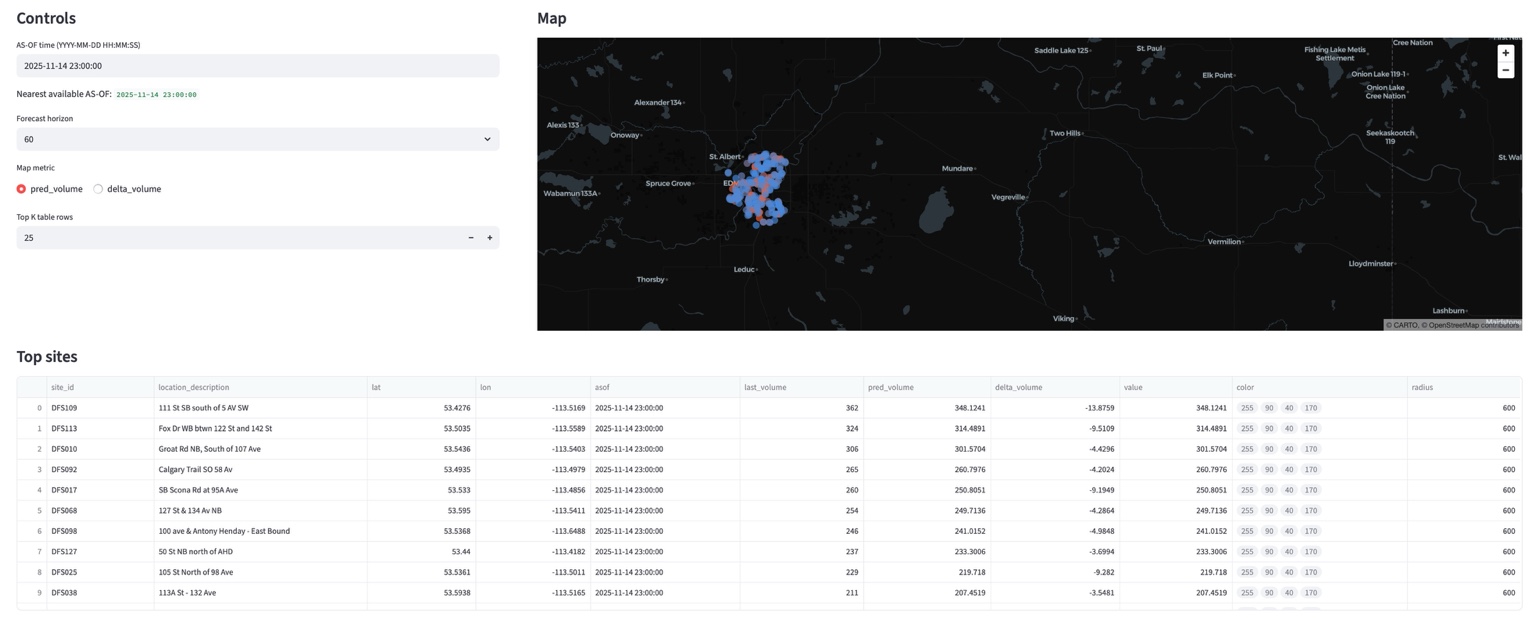
MAP + RANKING

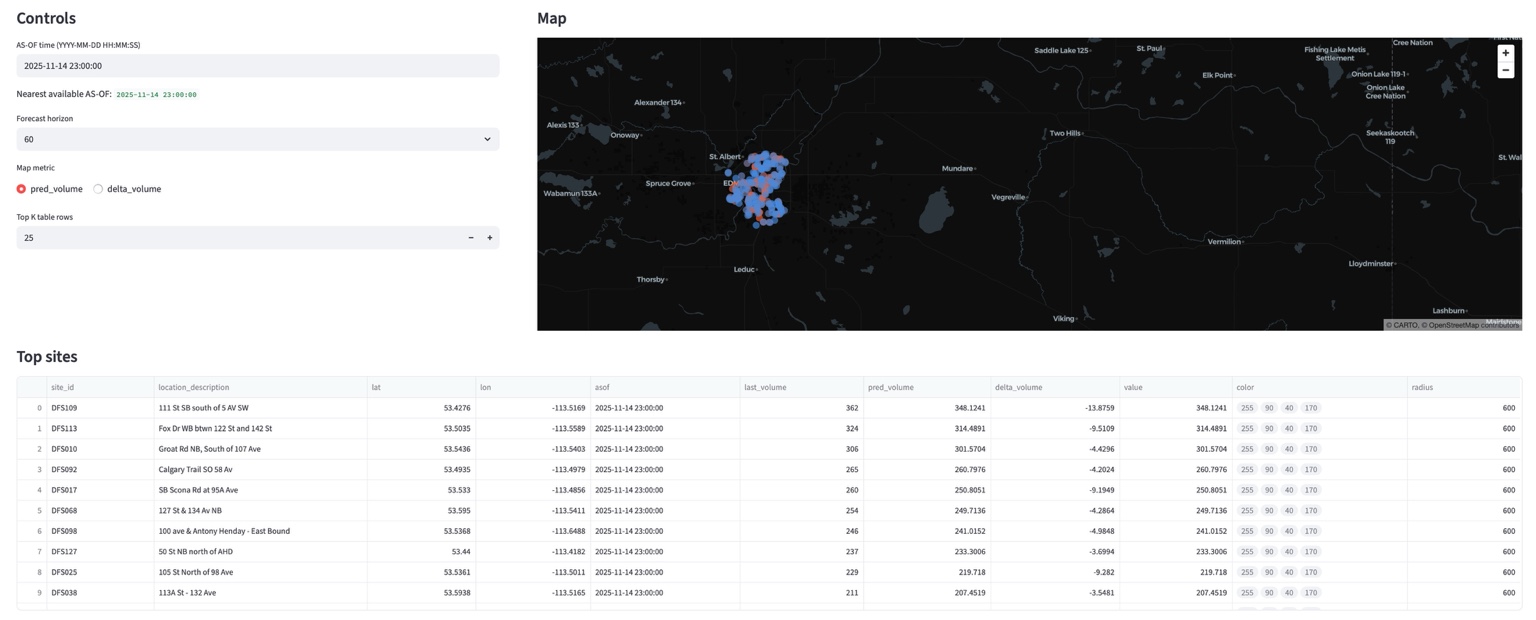
Once the model produced per-site forecasts, I generated outputs for visualization:

The map displays sensor sites as dots, where color/size encode predicted value (or delta). Hover reveals site metadata and forecast values.

This was the only part that felt like an application: not because it was accurate, but because it existed.

Figure 5 - 'Live-ish' Forecast Map (Conceptual View)

LIMITATIONS

CONCLUSION

This project did not produce a useful traffic oracle. It produced a pipeline that runs, forecasts that plot, and a quantitative reminder that many real systems are mostly inertia with brief exceptions.

Two years ago, GNNs were just words. Now they are a word attached to specific bugs, specific baselines, and a specific kind of disappointment.

Traffic is relational. But so is failure: it propagates, it persists, and it looks almost identical to yesterday unless something forces it to change.